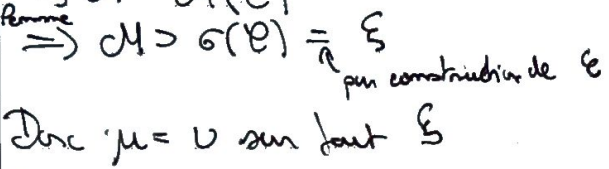Théorème de Dynkin - Math'φsics

Théorème de Dynkin

Formulaire de report
Problème d'affichage Contenu de la note peu pertinent

Théorème
Lemme de classe monotone, Théorème de Dynkin :
\(\mathcal C\) est stable par intersection

$$\Huge\iff$$

La Tribu et la Classe monotone engendrés par \(\mathcal C\) coïnci dent. $$\mathcal M(\mathcal C)=\sigma(\mathcal C)$$
(Pi-système, Lambda-système)

Corollaire : unicité de la mesure
Unicité de la mesure (corollaire du lemme de classe monotone/théorème de Dynkin) :
\((E,\mathcal E)\) est un Espace mesurable

\(\mathcal C\subset\mathcal E\)

\(\mathcal C\) est stable par intersection finie

\(\sigma(\mathcal C)=\mathcal E\)

$$\Huge\iff$$

deux Mesure de probabilités sur \(\mathcal E\) qui coïncident sur \(\mathcal C\) sont égales
Démontrer le théorème d'unicité de la mesure (corollaire du théorème de Dynkin/lemme de classe monotone).

Définir l'ensemble où les mesures coïncident.

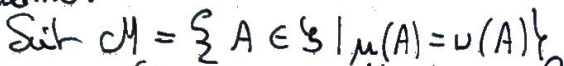
C'est une Classe monotone qui contient \(\mathcal C\).

Donc il contient la clase monotone engendrée par \(\mathcal C\).

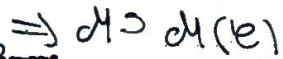
Par Dynkin, ça coïncide donc sur tout \(\mathcal E\).
Rétroliens :
- Mesure produit